Infinite Sequences in Clojure
Clojure has many interesting features that allow you to approach certain problems differently than you might in other languages. For example, by default most of the functions in the sequence library are lazy, which makes lazy sequences very common in Clojure.
For a lazy sequence, computation is deferred until its elements are realized. One of the consequences of laziness is that lazy sequences can be infinite, which allows for some interesting possibilities.
The example below is from iterate’s clojuredocs page. The powers-of-two is
actually an infinite sequence. However, this sequence clearly isn't being
realized when it's defined since all of the powers of two aren't something that
fit into memory! Instead, when an element of the sequence is requested, a
'chunk' (32 elements) of the sequence is realized.
(def powers-of-two (iterate (partial * 2) 1))
(nth powers-of-two 10)
;1024
(take 10 powers-of-two)
;(1 2 4 8 16 32 64 128 256 512)
Working with Clojure’s infinite sequences reminded me of an algorithm for sampling from streams of data called reservoir sampling. The reservoir sampling algorithm describes a procedure for selecting an equal probability sample from a stream of data of unknown length. This means that even if the stream of data were infinite (Clojure sequences I'm looking at you!), the algorithm could be halted at any point in time, and every element observed up to that point would have had an equal chance of being included in the sample.
Sampling
A sample for which each element has an equal probability of being selected is said to be an unbiased sample. Obtaining an unbiased sample is important because the goal of sampling and much of statistics is to use a subset of data (the sample) to draw conclusions about all of the data (the population). If certain elements are more likely to be chosen than others, a sample is said to be a biased sample. A biased sample increases the risk that conclusions drawn from its data will only pertain to the sample and not the population. This not only defeats the purpose of sampling, but also weakens and possibly invalidates any conclusions drawn from subsequent analyses based on the sample.
Below is a very famous example of sampling bias that occurred during the 1948 presidential election summarized by Wikipedia:
On election night, the Chicago Tribune printed the headline DEWEY DEFEATS TRUMAN, which turned out to be mistaken. In the morning the grinning president-elect, Harry S. Truman, was photographed holding a newspaper bearing this headline. The reason the Tribune was mistaken is that their editor trusted the results of a phone survey. Survey research was then in its infancy, and few academics realized that a sample of telephone users was not representative of the general population. Telephones were not yet widespread, and those who had them tended to be prosperous and have stable addresses.
Simple Random Sampling
In order to understand why reservoir sampling might be useful consider the following problem.
Let \( A \) be an array of data with \( N_a \) total elements (where \( N_a \) is large). We want to select an unbiased sample of \( k=100 \) elements from \( A \). This means that each element in \( A \) has to have \( \approx \frac{100}{N_a} \) chance of being selected. Another way of saying this is that if we were to repeat our sampling procedure for many trials, each element would be selected as part of the sample in about the same number of trials.
For a population like \( A \) with a known number of elements an easy way of obtaining an unbiased sample is a procedure known as simple random sampling. Simple random sampling works as follows:
Randomly choose 100 numbers between 1 and \( N_a \) and then select each element whose index corresponds to the numbers chosen (if an elements index is selected twice we just draw again). We can see that such a sample is unbiased, since each element has 100 opportunities to be selected and for each opportunity there is \( \frac{1}{N_a} \) chance of being selected, which implies each element has \( \frac{100}{N_a} \left(\text{or } \frac{k}{N_a} \right) \) probability of being included in the sample.
The Reservoir Sampling Algorithm
However, now imagine that instead of an array of fixed size, we instead have a stream of data \( S \) of unknown length \( N_s \). We still want each element to have an equal chance of being selected into the sample, except now since \( N_s \) is unknown the simple random sampling procedure no longer works. We could store all of the records and then when the stream terminates apply the simple random sampling procedure. However, this would require storing every record and waiting for \( S \) to terminate.
Rather than storing the elements and waiting for \( S \) to terminate, reservoir sampling instead describes a procedure for making an accept or reject decision as each element of \( S \) arrives, while still guaranteeing that whenever the stream does terminate each element in the stream will have had a \( \frac{k}{N_s} \) probability of being included in the sample. This is despite the fact that \( N_s \) was unknown until after the stream terminated.
Below is a description of the reservoir sampling algorithm:
- Create an array of size \( k \) (the reservoir) and add the first \( k \) elements of the stream \( S \).
- Then as each new element in \( S \) arrives, generate a random number \( j \) between 1 and the number of elements observed so far. If \( j \) is less than or equal to \( k \), replace element \( j \) in the reservoir with the new element.
That's it. However, it’s not immediately obvious that this would accomplish what we want, but it's not too difficult to prove that each element has probability \( \frac{k}{N_s} \) of being included in the sample and that reservoir sampling thereby produces an unbiased sample.
Proving Reservoir Sampling Results in an Unbiased Sample
The \( i_{th} \) element is included in the sample whenever our random integer \( j \leq k \), which occurs with probability \( \frac{k}{i} \). Recall, there are \( k \) total elements in the reservoir and \( i \) is the number of elements observed up to this point in the stream. The probability of any integer between 1 and \( i \) being selected is just \( \frac{1}{i} \). This includes the indices associated with the \( k \) elements currently in the reservoir, which implies that the probability of removing a specific element from the reservoir during a given round is also \( \frac{1}{i} \). Therefore, the probability that an element already in the reservoir doesn't get removed during a particular round is \( 1 - \frac{1}{i} \).
Using the result above, reservoir sampling can then be shown to work for an arbitrary length stream via induction.
-
The base case is true since for a stream with only \( k \) elements each element is selected with probability of 1 \( \left(\frac{k}{k} = \frac{k}{N}\right ) \).
-
For the inductive step, assume for a stream of length \( N \) the probability of any element being selected is \( \frac{k}{N} \), then it needs to be shown that for a stream of length \( N + 1 \) each element has a probability of being selected of \( \frac{k}{N + 1} \).
We know that the new element \( N + 1 \) will only be included in the sample if our random number \( j \) is less than or equal to \( k \) (remember \( j \) ranges from 1 to \( N + 1 \)), so that will happen with probability \( \frac{k}{N + 1} \).
For the elements that are already in the sample we can use the inductive hypothesis combined with the probability that an existing element will not be removed to show their inclusion probability is also \( \frac{k}{N + 1} \)
\begin{align*}
&= \frac{k}{N} * \left(1 - \frac{1}{N + 1}\right) \
&= \frac{k}{N} * \left(\frac{N}{N + 1}\right) \
&= \frac{k}{N+1}
\end{align*}
which proves the result for streams of arbitrary length.
Reservoir Sampling in Clojure
Below is my Clojure implementation of the reservoir sampling algorithm. Writing this in Clojure was fun, since its declarative style allows for writing code that reads almost exactly like the algorithm's description above.
(defn add-element-to-reservoir [reservoir element]
(conj reservoir element))
(defn replace-element-in-reservoir [reservoir old-element-indx new-element]
(assoc reservoir old-element-indx new-element))
(defn reservoir-sample
([stream k] (reservoir-sample stream 1 k []))
([stream round reservoir-size reservoir]
(let [j (rand-int round)
current-element (first stream)
remaining-stream (rest stream)]
(cond
(empty? stream) reservoir
(< (count reservoir) reservoir-size)
(recur remaining-stream (inc round) reservoir-size
(add-element-to-reservoir reservoir current-element))
(< j reservoir-size)
(recur remaining-stream (inc round) reservoir-size
(replace-element-in-reservoir reservoir j current-element))
:else
(recur remaining-stream (inc round) reservoir-size reservoir)))))
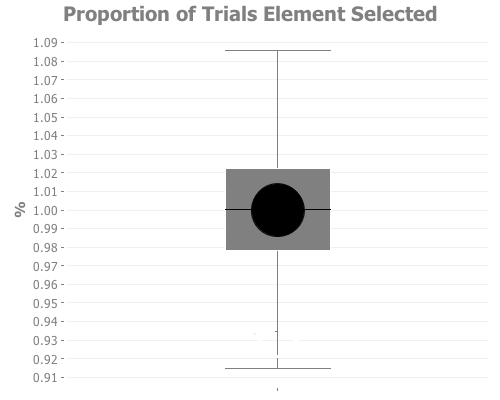
To confirm that the algorithm works as expected, I simulated 100,000 trials using the reservoir sampling algorithm to select 10 elements from a stream of 1000 and then counted the proportion of trials in which each element was selected. If things are working as expected, we'd expect to see each element being selected in \( \approx 1% \) of the trials \( \left(\frac{10}{1000}\right) \).
(defn selection-probabilities [trials reservoir-size stream-length]
(let [trial-results
(frequencies
(apply concat (repeatedly trials #(reservoir-sample (range stream-length) reservoir-size))))]
(into (sorted-map) (for [[k v] trial-results] [k (float (/ (* 100 v) trials))]))))
I used the Clojure library incanter along with a box plot to summarize the results. The results look more or less like what we'd hope if the algorithm is working correctly. The selection probabilities for each element are tightly centered around 1%.
(use '(incanter core stats charts io))
(def plot
(box-plot
(vals (selection-probabilities 100000 10 1000))
:category-label ""
:x-label ""
:title "Percent of Trials Each Element Was Selected"
:y-label "%"))
(view
(set-theme-bw plot))
Like I said earlier, I'm really enjoying the declarative way that Clojure code is written. You can almost do a word for word transcription of an algorithm to code and assume that it will just work. It's also nice because the declarative style allows you to think about the problem that you're trying to solve using almost the same abstractions and terminology in both the problem description and the code, rather than bouncing between various levels of abstraction. Overall, I’m enjoying the experience so far and looking forward to learning more.
